(Copyright Hew Wolff, 2005.)
The Google Labs Aptitude Test is a delightful recruitment challenge that was released around September 2004. A team of Mathematica experts has come up with solutions to the more mathematical problems. They skipped problem 19, though, which is an interesting one. Here I present solutions to that problem.
The original problem is:
'Tis known in refined company, that choosing K things out of N can be done in ways as many as choosing N minus K from N: I pick K, you the remaining. Find though a cooler bijection, where you show a knack uncanny, of making your choices contain all K of mine. Oh, for pedantry: let K be no more than half N.
First to restate the problem in modern English. Suppose K and N are integers with 0 <= K <= N / 2. Suppose X is a set with N elements, XK is the set of subsets of X with K elements, and XN - K is the set of subsets of X with N - K elements. Obviously XK and XN - K have the same size, namely N choose K. Then find a bijection b from XK to XN - K such that S is a subset of b(S) for all S in XK.
The case N = 0 is trivial.
The case K = N / 2 is also trivial:
I know of three solutions.
Solution 1 is short but not quite satisfying. It uses a basic result from combinatorics, Hall's marriage theorem. That theorem gives us a proof of existence rather than a construction, so this solution may not meet the original criteria, although the theorem has constructive proofs which we could presumably use to construct our b.
Solution 2 uses a nifty construction of de Bruijn, a decomposition of the lattice of subsets of X into "symmetric chains". (Thanks to Torsten Sillke for showing me this.)
Solution 3 is a more elaborate but elementary construction that I worked out.
Naturally all this leads to more Questions.
Construct a bipartite graph G on the union of
Suppose P is a subset of
This claim allows us to invoke Hall's
marriage theorem, which says that there is a "complete matching"
from
Here I will build up the proof starting from the concept of a lattice, based on the treatment in Loeb, Damiani, and D'Antona's paper. All of our sets will be finite.
Given x and y in a lattice, y "covers" x if y is a minimal element greater than x. A "ranking" of the lattice is a function r with r(m) = 0 for the minimum element m, and r(y) = r(x) + 1 when y covers x. For example, the lattice 2X of subsets of X has the obvious ranking taking a subset to the size of that subset.
A "chain" in a ranked lattice is a sequence of elements
x0, ..., xn where each
xi + 1 covers xi.
The chain is "symmetric" if its minimum and maximum elements have the same total rank as the lattice itself:
r(x0) + r(xn) =
r(M), where M is the maximum of the lattice. For example, in the lattice 2X defined above, the
sequence {0},
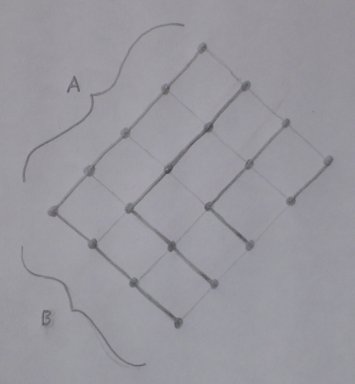
A "symmetric decomposition" of a lattice is a partition into symmetric chains. As a trivial example, a lattice consisting of one chain has a symmetric decomposition consisting of the entire lattice itself. But here's the interesting example. If A and B are chain lattices, then it turns out that their product lattice A × B has a nice symmetric decomposition too. As an easy exercise, write down a proof based on this diagram:

In fact we can say more. If A and B are any lattices with symmetric decompositions {Ai} and {Bj}, that last fact gives us a nice symmetric decomposition for A × B, as follows. First partition the product lattice into {Cij = Ai × Bj}. Pick one Cij. It's a product of two chains, so it has a symmetric decomposition as above, say {ck}. Each ck is symmetric in Cij, and Cij is symmetric in A × B, so each ck is symmetric in A × B, and the set of all ck is a symmetric decomposition of A × B.
But the lattice 2X is a product of chains, because it's isomorphic to {0, 1}N. (We can visualize it as a hypercube standing on its corner.) So the construction above gives a symmetric decomposition {ck} of 2X. Now go back to the level sets XK and XN - K. Because of the symmetry property, ck meets XK if and only if ck meets XN - K, and the intersection in both cases is a single element. This gives us our bijection.
Suppose we're given S in XK; our job is to define b(S). First we define a function g inductively as follows: g(0) = 0;
g(i + 1) =
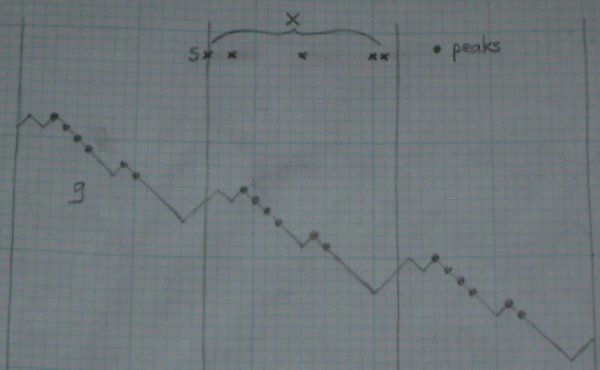
For example, if N = 16, K = 5, and S = {0, 2, 8, 14, 15}, then g looks like the picture below, and T = {3, 4, 5, 6, 9, 10}. (Pardon the crude graphics; I don't have a copy of Mathematica lying around.) You see that I've extended g to the negative integers, using the same equations as above.
Now for the proof. I'll divide this into two claims: (1) that the union of S and T has N - K elements, which means that b is a map from XK to XN - K; and (2) that S can be reconstructed from the union of S and T, which means that b is one-to-one and therefore a bijection.
Note that for any N consecutive numbers, K of them will be in S (mod N), and N - K of then will not be in S (mod N). So
(*) For all i, g(i + N) = g(i) - (N - 2K).
To prove (1), we need to understand peaks better. Use the picture above as a guide for the following discussion.
g reaches some maximum value r on X. Partition the integers into translates of X, namely X + aN for all integers a. From (*), the maximum value of g on X + aN is r - a(N - 2K). So, as i approaches infinity, g(i) approaches negative infinity; and similarly as i approaches negative infinity, g(i) approaches infinity.
This means that for any j, g reaches the value j at least once, but only a finite number of times. So we can define a function p as follows: p(j) is the largest number i for which g(i) = j. p(j) must be a peak: if g rises at least as high as as j anywhere to the right of p(j), then g must also reach the value j again, which is against the definition of p. We can call j the "height" of the peak. Moreover, all peaks arise in this way: i = p(g(i)) if and only if i is a peak. It's clear that g(p(j)) = j for all j. To put it differently, if we take the peak points in the graph of g and reflect them in the line y = x, we get the graph of p.
Going back to the the maximum value r of g on X,
it's now clear that p(r) is a peak in X, since g
never reaches r again to the right of X. In fact,
p(r) is the first peak in X, because any peak to the
left of it would have to have be higher, and r is the maximum.
Also, it's easy to see that i is a peak if and only if i
+ N is a peak, because (*) says that shifting the graph of
g over by N is the same as shifting it vertically, which
leaves the peaks unchanged. So p(r) + N is the first
peak in X + N. From (*), the height of this peak is
Moreover, from the definition of g, a peak in X cannot be in S. So the set T of peaks in X is disjoint from S and has N - 2K elements, which means that the union of S and T has N - K elements. This establishes claim (1).
Now we need to prove claim (2). Suppose we are given the union U of S and T. Define a "mirror-image" function m by m(i) = N - 1 - i. Note that m2 = 1, m(i mod N) = m(i) mod N, and m(X) = X. Take S' = m(X - U), which is is a subset of X with K elements. Just as we did with S above, we can use S' to get a function g' with its own set T' of peaks in X. Now I claim that T' = m(T). This is enough to prove (2), because we can now recover T = m(T') and S = U - T. So we just need to prove that T' = m(T).
Here's a picture of g' for the example above, which you can compare with g.
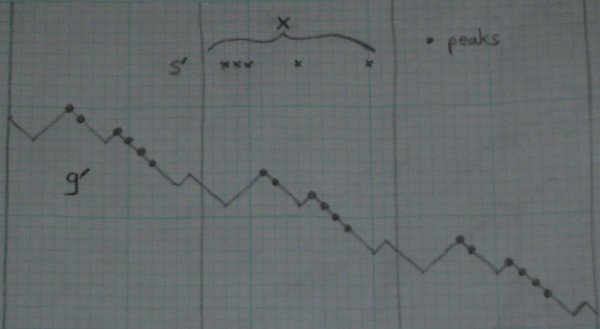
Go back to g, and consider the numbers which are not peaks. Partition these numbers into maximal consecutive sequences, and call these valleys. Take one valley V = [v0, v1) (that is, {i: v0 <= i < v1}). v0 - 1 and v1 are consecutive peaks, so g(i) <= g(v1) = g(v0) for all i in V.
Let
i range from v0 to v1, and consider what happens to
g(i) and g'(m(i) + 1) as we do
this. As we go from i to
This means that g'(m(i)) <= g'(m(v1)) = g'(m(v0)) for all i in V, and therefore g' has no peaks in V' = m(V). So if i is a valley point for g, then m(i) is a valley point for g'. But g and g' have the same number of valley points in X, because S and S' have the same size, so all valley points of g' arise in this way. So the points that don't lie in any V' = m(V) are exactly the peaks of g'. So m(T) = T', as claimed above.
This proves claim (2), so the proof is complete.
By the way, it's clear from the proof that if you want to know whether t is a peak, you don't need to make the infinite sequence of tests suggested by the definition. You only need to check whether g(i) < g(t) for all i in [t + 1, t + N). So the function b is easy to compute.
Are there any references for this precise result?
How many such bijections b are there? How can we describe them all?